Wednesday, 8 April 2015
INTRODUCTION TO AUTOMATA THEORY
Before we begin let me put some light on ABSTRACT MACHINES.
An Abstract Machine is the theoretical model of basic computer attributes,more specifically computer hardware or software.These Abstract machines functions on the concept of Discrete Times.
Discrete time visualize the value of the entity occurring at discrete(distinct)places in time.Abstract
Machines had all the capabilities of present computers,more precisely what they could compute.These abstract machines became the basis of Turing's study.Turing's purpose was to define a boundary of what a machine could compute and what not.
Finite Automata(simpler machines) were studied by number of computer scientists proved to be useful in number of purposes.The formal grammar studied bt N Chomsky served the basis for various software components and important parts of compiler especially Lexical Analyzer.
Later S.Cook was able to take Turing's concept to the goal.He was able to distinguish between the problems that a computer could solve efficiently and the problems that could be solve in a principle but could consume a lot of time.These problems are referred to as intractable problems.
These developments in theoretical computer science enable us perceive what we can expect from software.Well the theory of intractable problems help us to judge the approach of problem solving i.e. whether we have to approach a certain problem head-on or we have to write a program to solve it(as it does not belong to intractable class) or we have to find another way or heuristic to counter a intractable problem so that we could limit the amount of time computer spend on solving such kind of problem.
THE FINITE AUTOMATA
These are a useful model for various kinds of computer software and hardware.Some of the important uses are :-
1. Software for designing and testing the behavior of digital components.
2. Software for searching large texts,such as collection of web pages, to figure out the occurrences of words,phrases,any sequence or patterns.
3.Software for testing all systems that have finite number of discrete states(Since it is finite automata),such as communication protocols,protocols for security purpose i.e.to ensure secure exchange of information.
4.The lexical analyzer of a typical compiler also examples the use of finite automata.
Lexical Analyzer is that part of a compiler which breaks the text into logical units such as identifiers,keywords and punctuation.
The above systems may be seen as being in one state at all times in a finite set of states.
Still thinking what's the use in developing such kind of theoretical concepts..............Let just summarize the utility of the above concept.
Well this theoretical part of computer science makes us develop the art of designing machines.
As we know we got finite number of states(The utility of state is to remember the relevant part of computer or process history) hence finite remembering capability,hence a machine should be designed very carefully in such a way that it just remembers what is important ad forget what is not.
Now the question arises why we use only finite number of states?we can have as many states as we want then whats the fun in using finite states.....
Answer to this is.......By using a fixed and finite number of states we can run a system with a fixed set of resources.
Have a look at this example..........
1. Software for designing and testing the behavior of digital components.
2. Software for searching large texts,such as collection of web pages, to figure out the occurrences of words,phrases,any sequence or patterns.
3.Software for testing all systems that have finite number of discrete states(Since it is finite automata),such as communication protocols,protocols for security purpose i.e.to ensure secure exchange of information.
4.The lexical analyzer of a typical compiler also examples the use of finite automata.
Lexical Analyzer is that part of a compiler which breaks the text into logical units such as identifiers,keywords and punctuation.
The above systems may be seen as being in one state at all times in a finite set of states.
Still thinking what's the use in developing such kind of theoretical concepts..............Let just summarize the utility of the above concept.
Well this theoretical part of computer science makes us develop the art of designing machines.
As we know we got finite number of states(The utility of state is to remember the relevant part of computer or process history) hence finite remembering capability,hence a machine should be designed very carefully in such a way that it just remembers what is important ad forget what is not.
Now the question arises why we use only finite number of states?we can have as many states as we want then whats the fun in using finite states.....
Answer to this is.......By using a fixed and finite number of states we can run a system with a fixed set of resources.
Have a look at this example..........
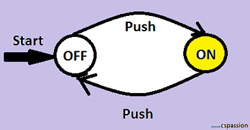 |
| A FINITE AUTOMATA MODELLING ON/OFF SWITCH |
The above example models a finite automaton of an on/off switch.Here we've got only one switch.The system need to remember the current state i.e. whether the switch is on or off and perform the opposite of the current state whenever the switched is pushed.
The system goes on as follows:-
- Initially the system is in 'OFF' state,when the switch is pressed it transits to 'ON' state.
- Now when the system is in 'ON' state and again the switch is pushed it transits back to 'OFF' state.
This is the simple case of finite automaton as remembering the current behavior or current state is quite easy.But sometimes its really complex to remember the behavior associated with system.
Let us view another example.......
The above example depicts how a lexical analyzer recognizes a keyword.Here in this example keyword'else' is recognized.
This automaton needs five states to work on,each state representss a checkpoint or a position in the keyword that has been reached so far.
The system works on as follows:-
- The system starts with an empty string.
- Lexical Analyzer is imagined to compile each character one by one.
- The input character along with previous state character is remembered at each and every state as the system progresses.
- Since it is the work of automaton to check when the desired keyword is fully processed and make that state the accepting state.
Hence automata is essential for resolving following two big issues in the field of computer science:-
1. DECIDABILITY:-
This addresses what a computer can do actually.The problems which can be resolved by computer are referred to as 'decidable'
2.INTRACTABILITY;-
This addresses what a computer can do efficiently.The problems that can be faced by computer head on or in finite or certain period of time with respect to the input are referred to a 'tractable'.
This was a Introduction to Automata Theory.........
This was a Introduction to Automata Theory.........
Subscribe to:
Post Comments (Atom)
Search
Popular Posts
-
Troubleshooting Cisco VPN client Before starting troubleshooting, Let us see what VPN is and what it requires to perform its intended f...
-
File Versioning C# File versioning, saving file with unique file name in c# File versioning allows a user to have several versions of ...
-
Evolution-Mobile Phones With the development of portable technology,wireless communication has so evolved that (According to the announce...
-
Text Box Hint in c# Windows Form Application Text Box Hint in c# Windows Form Application While developing a windows form applicat...
-
Unable to set the Freeze Panes property of Window Class C# It is generally easy to resolve the compile time errors because the reason fo...






52FAC8B8FE
ReplyDeleteuygun instagram takipçi
Türkiye Posta Kodu
Erasmus Proje
Pubg New State Promosyon Kodu
Azar Elmas Kodu
İnstagram Kaydedilenler Toplu Silme
Hay Day Hile Kodları
Minecraft Hile Kodları
henry modern swivel accent chair